Bayesian Experimental Design for Model Discrepancy Calibration: An Auto-Differentiable Ensemble Kalman Inversion Approach

Bayesian experimental design (BED) offers a principled framework for optimizing data acquisition by leveraging probabilistic inference. However, practical implementations of BED are often compromised by model discrepancy, i.e., the mismatch between predictive models and true physical systems, which can potentially lead to biased parameter estimates. While data-driven approaches have been recently explored to characterize the model discrepancy, the resulting high-dimensional parameter space poses severe challenges for both Bayesian updating and design optimization. In this work, we propose a hybrid BED framework enabled by auto-differentiable ensemble Kalman inversion (AD-EKI) that addresses these challenges by providing a computationally efficient, gradient-free alternative to estimate the information gain for high-dimensional network parameters. The AD-EKI allows a differentiable evaluation of the utility function in BED and thus facilitates the use of standard gradient-based methods for design optimization. In the proposed hybrid framework, we iteratively optimize experimental designs, decoupling the inference of low-dimensional physical parameters handled by standard BED methods, from the high-dimensional model discrepancy handled by AD-EKI. The identified optimal designs for the model discrepancy enable us to systematically collect informative data for its calibration. The performance of the proposed method is studied by a classical convection-diffusion BED example, and the hybrid framework enabled by AD-EKI efficiently identifies informative data to calibrate the model discrepancy and robustly infers the unknown physical parameters in the modeled system. Besides addressing the challenges of BED with model discrepancy, AD-EKI also potentially fosters efficient and scalable frameworks in many other areas with bilevel optimization, such as meta-learning and structure optimization.

Data-Driven Stochastic Closure Modeling via Conditional Diffusion Model and Neural Operator

Closure models are widely used in simulating complex multiscale dynamical systems such as turbulence and the earth system, for which direct numerical simulation that resolves all scales is often too expensive. For those systems without a clear scale separation, deterministic and local closure models often lack enough generalization capability, which limits their performance in many real-world applications. In this work, we propose a data-driven modeling framework for constructing stochastic and non-local closure models via conditional diffusion model and neural operator. Specifically, the Fourier neural operator is incorporated into a score-based diffusion model, which serves as a data-driven stochastic closure model for complex dynamical systems governed by partial differential equations (PDEs). We also demonstrate how accelerated sampling methods can improve the efficiency of the data-driven stochastic closure model. The results show that the proposed methodology provides a systematic approach via generative machine learning techniques to construct data-driven stochastic closure models for multiscale dynamical systems with continuous spatiotemporal fields.

Vision-Based Target Localization for a Flapping-Wing Aerial Vehicle

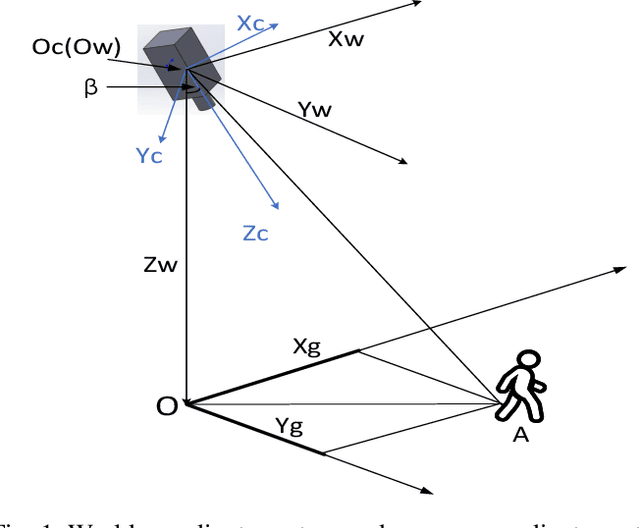
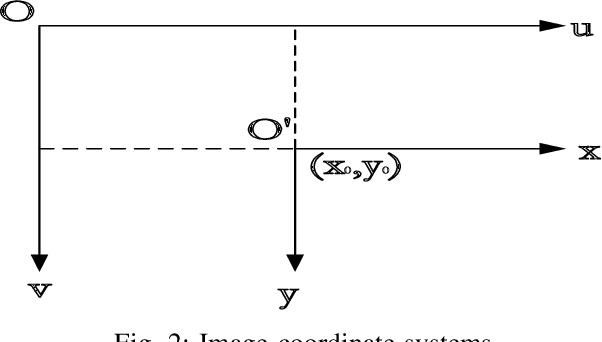
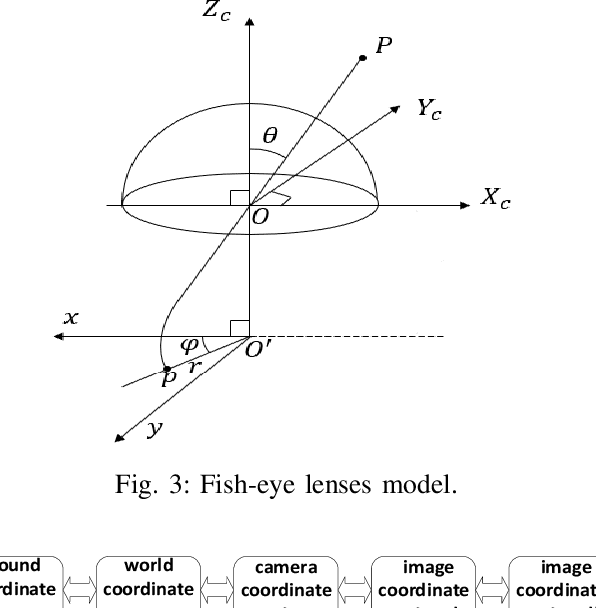
The flapping-wing aerial vehicle (FWAV) is a new type of flying robot that mimics the flight mode of birds and insects. However, FWAVs have their special characteristics of less load capacity and short endurance time, so that most existing systems of ground target localization are not suitable for them. In this paper, a vision-based target localization algorithm is proposed for FWAVs based on a generic camera model. Since sensors exist measurement error and the camera exists jitter and motion blur during flight, Gaussian noises are introduced in the simulation experiment, and then a first-order low-pass filter is used to stabilize the localization values. Moreover, in order to verify the feasibility and accuracy of the target localization algorithm, we design a set of simulation experiments where various noises are added. From the simulation results, it is found that the target localization algorithm has a good performance.